finl is not LaTeX

Building a trie in Rust—optimizations

September 30, 2021 by Don Hosek

A trie is a variation on a tree whose purpose is to show the result of a sequence of values, something that I’ll be using a lot in finl. For example, TeX has a number of input conventions implemented via ligatures (plus an active character) that I’ll be making optionally available through a character substitution mechanism. The trie for this looks like:

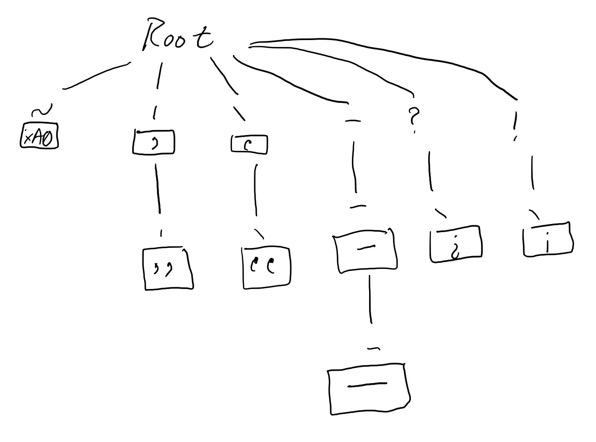
The implementation of this is to have each node in the trie consisting of a map of characters to nodes and an optional substitution text. 

The obvious choice of what to reach for as a map is a hash map of some sort, but Rust makes things interesting in that the hashing function is easily configurable¹ so I decided to do some experimenting since the default hasher is heavier weight than I need and with the char sub algorithm, nearly every single character in the file will end up getting hashed at least once.² I don’t need to worry about hash DOS attacks or cryptographic strength in this situation so the default hasher SipHasher13 is overkill. The recommended alternative for short keys is FNVHasher from the fnv crate, so I set up a benchmark that runs a collection of Dickens stories in TeX format against the TeX character substitution table to run benchmarks. As expected, I saw an improvement of 24%. But I wondered if I could do better. In particular, since my keys are a simple type and guaranteed to be less than 24 bits. Perhaps even an identity hasher would make sense in this case.

And then writing that last sentence, I remembered, hash collisions. I once interviewed for Amazon³ and having heard they liked to ask a lot of data structure books, I read a data structures book the week before the interview, so I have a good idea of what happens below the hood with a hash map: Essentially, you’re creating an array of keys and pointers to your stored data and you take the hash value, mod it the size of the array, then look at the resulting point element in the array. If it’s empty, there’s no match. If it’s not, you then check the keys for equality. Here’s where things get tricky: If they’re equal, you’re done, but if they’re not, you need to then iterate through the array until you either get equality, reach an empty element in the array or finish the array.

And Rust’s implementation of this is… not great in this respect. For an application like my trie, I want to fail fast on lookup, but Rust will happily fill its entire capacity before resizing on insert. This is one place where Java wins: It allows users of HashMap to specify a load factor (0.55 by default) so that rather than resizing when the capacity is filled, it resizes once you have capacity × load factor elements inserted. Since I’m expecting most lookups in the trie to fail, it’s better to fail faster. I boosted the initial capacity of the map to 64 and the benchmark improved by 53% (one small optimization I made was to only specify an initial capacity for the root map of children. For this application, at least, once we’re starting down a trie, the possible matches are a smaller set and there’s less danger of there being a significant cost to false positives).

But one more thing. My keys are short and of constant size. Maybe I could get better performance with a simpler hashing function. I tried creating a simple null hasher that just used the value passed in:

impl Hasher for NullHasher {
    fn finish(&self) -> u64 {
        self.0
}

    fn write(&mut self, bytes: &[u8]) {
        self.0 = bytes.iter()
            .take(7)
            .rfold(0u64, |acc, x| acc * 256 + *x as u64);
    }

    fn write_u32(&mut self, i: u32) {
        self.0 = i as u64;
    }
}

and was surprised to discover that, in fact, things slowed down, apparently because of cleverness in the Swiss Tables algorithm that I don’t fully understand. So, without doing a full hash table algorithm using a simple mod trick, it looks like FNV + capacity is my best bet for performance at the moment. 

1. Coming from Java this is a bit of a shock since Java’s HashMap can only use the hash() function of the key. If you want a custom hasher for a key, you need to create a custom class for the key with a new hash() function. But since common key types like String or Char are declared final, you can’t just subclass the type and override hash, you need to create a wrapper class instead. 
2. One of the interesting challenges in writing the char sub algorithm was dealing with mappings like A→a, ABC→b where an input like ABD should get mapped to aD which meant that in that instance, we need to backtrack on the input and A and B end up getting hashed twice in that scenario.
3. They said no.

Comments |0|

This site uses Akismet to reduce spam. Learn how your comment data is processed.